모델의 애니메이션을 위해서 각 프레임의 변환(transform)정보를 가지고있어야 한다. 하지만 모든 프레임에 대한 변환 정보를 저장하기에는 비용이 너무 크다. 때문에 몇몇 'key frame' 에 대한 변환 정보만을 저장하고 중간의 정보는 이들 key frame을 보간하여 생성하게된다.
이번 글에선 이들 변환 정보중 회전변환의 보간에 대해서 설명하려 한다.
애니메이션의 회전변환은 회전행렬의 보간시 발생하는 심각한 문제 때문에 사원수로 표현해야만 한다.
두 사원수 [math]\mathbf{p}[/math]와 [math]\mathbf{q}[/math]의 보간은 단위길이 1의 구체에서 이 두 사원수가 표현하는 지점의 최단거리 호(shortest arc)상의 지점을로 나타나게 된다.
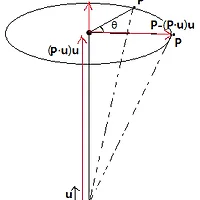
[math]0\le t \le 1[/math]인 정규화된 파라미터 [math]t[/math]에 대하여 두 사원수를 보간하면 위 그림과 같은 결과를 갖게된다.
보간된 결과를 [math]\mathbf{r}[/math]라 하면
[math!]\mathbf{r} = n\mathbf{p} + m\mathbf{q}[/math!]
가 그 값이된다. [math]n[/math]의 값을 먼저 구해보자. [math]h = n\sin\theta[/math]로 부터 [math]n=\frac{h}{\sin\theta}[/math]를 구할 수 있다. 위 원은 단위구로 부터의 대원(great circle) 이므로 반지름은 1이다. 즉, [math]h=\sin\theta(1-t)[/math]이므로 [math]n[/math]는 다음의 값을 가진다.
[math!]n=\frac{\sin\theta(1-t)}{\sin\theta}[/math!]
비슷한 방법으로 [math]m[/math]의 값 또한 계산할 수 있다.
[math!]m=\frac{\sin\theta t}{\sin\theta}[/math!]
이를 정리하면 최종적으로 다음과 같이 표현된다.
[math!]\frac{\sin\theta(1-t)}{\sin\theta}\mathbf{p} + \frac{\sin\theta t}{\sin\theta}\mathbf{q}[/math!]
설명에서 보았듯, 두 사원수의 보간은 구면을 따라 보간되므로 흔히 구면 선형 보간(spherical linear interpolation)이라 불리며 slerp로 줄여 표현한다.
'Graphics Note' 카테고리의 다른 글
| rigid body collision 1 (0) | 2014.04.21 |
|---|---|
| automatic linking the first out variable of fragment shader (4) | 2014.04.02 |
| [Mathematics] rotation quaternion details (0) | 2014.03.28 |
| device context and rendering context (0) | 2014.02.24 |
| Bezier curve (0) | 2014.02.04 |